The Seven Laws of Origami
An exploration of the mathematical axioms that govern the ancient Japanese paper folding art.

Akira Yoshizawa, a teenager in the nineteen-twenties, quit his factory job and proceeded to turn paper-folding into a fine art. Today, origami kits are common and consist of a booklet of instructions and a set of colored paper. The paper is two-sided with a different color on each side. The instructions, consisting of mostly of arrows and lines, are a part of a worldwide standard of visual language for origami that Akira pioneered. He also invented the wet folding technique, which allows for more sculptural interpretations.
A new challenge for mathematicians is understanding the mathematical axioms that govern simple origami folds. In 1989, The First International Meeting of Origami Science and Technology, organized by Humiaki Huzita, unified paper folders and mathematicians together. In high school geometry, students are taught how to construct, using a compass and straightedge. A couple of classical geometrical problems have been proven unsolvable with this traditional method of using a compass and straightedge, traditional tools of high school geometry, has been proven inadequate for certain classical problems in geometry. however, Origami has provided a beautifully artistic solution.
Axiomatic Paper Folding

The magic of combining mathematics and origami
The Huzita-Justin, or Huzita-Hatori Axioms, were first discovered by Justin Jacques in his 1986 paper, translated from French as "Resolution by folding of the third degree equation and geometric applications." Humiaki Huzita rediscovered axioms one through six. D. Aukly and J. Cleveland rediscovered axioms one through five. Koshiro Hatori and Robert J. Lang separately rediscovered axiom seven.
Axiom One: Given two distinct points p1 and p2, there is a unique fold that passes through both of them.
Axiom Two: Given two distinct points p1 and p2, there is a unique fold that places p1 onto p2.
Axiom Three: Given two lines l1 and l2, there is a fold that places l1 onto l2.
Axiom Four: Given a point p1 and a line l1, there is a unique fold perpendicular to l1 that passes through point p1.
Axiom Five: Given two points p1 and p2 and a line l1, there is a fold that places p1 onto l1 and passes through p2.
Axiom Six: Given two points p1 and p2 and two lines l1 and l2, there is a fold that places p1 onto l1 and p2 onto l2.
Axiom Seven: Given one point p and two lines l1 and l2, there is a fold that places p onto l1 and is perpendicular to l2.
Axiom Five provides zero, one, or two solutions. Axiom Six provides zero, one two or three solutions. This compares notably to the geometry of compass and straightedge which provides a maximum of two solutions.
Solving the Delian Problem Using Origami
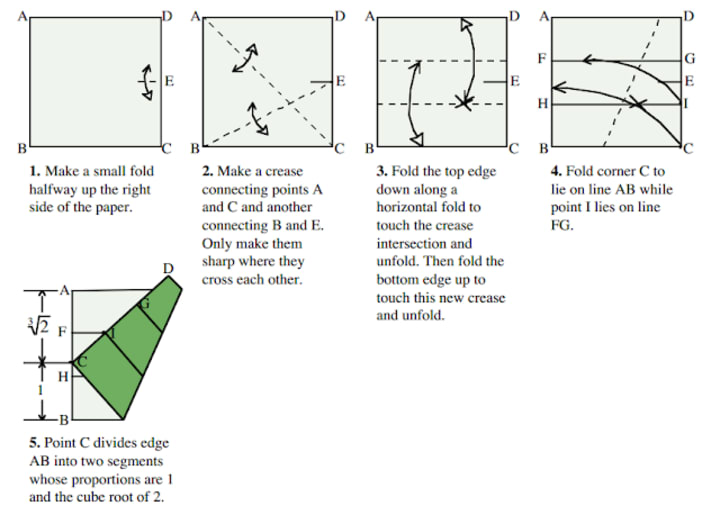
Doubling the cube by folding a square sheet of paper
Doubling the cube is an ancient geometric problem. Given the edge of a cube, the problem requires the construction of the edge with a length of a second cube such that the volume is double the volume of the first cube. The problem of doubling the cube, also known as the Delian problem, is solvable with an origami construction designed by Peter Messer. The edge with the crease mark is called a marked straightedge, which is not allowed in compass and straightedge constructions. The use of a marked straightedge in this way is called a neusis construction.
The problem supposedly arose from a story of Ancient Greece. Thousands of Athenians had been wiped out by a plague in 430 B.C. and so, a messenger was sent to consult the Oracle of Delos, who said that the doubling the volume of the altar would put an end to the plague. The form of the altar was a cube, and the Athenian foolishly doubled the length of the sides for the construction of the new altar. More people fell ill from the plague, and in their confusion, the distressed Athenians consulted Plato. He explained that the problem had nothing to do with the altar size, but with the Athenians's overall approach to geometry and mathematics. It was for their general misunderstanding of mathematics that the deities had been punishing them. By doubling the length of the sides of the altar, they did not actually double the volume of the cube. This is one of the problems that can be solved by origami, but not with a compass and straightedge.
The Trisection of an Angle Using Origami
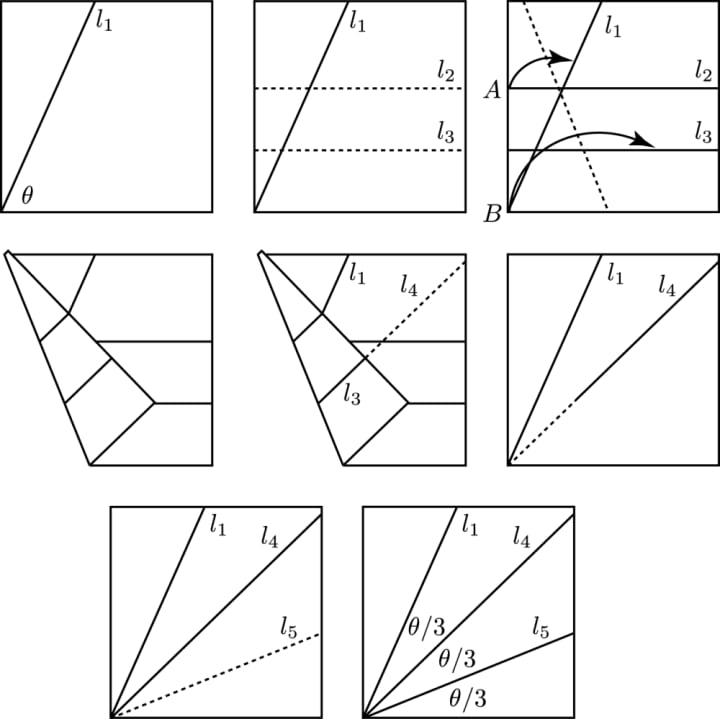
Trisecting an angle by folding a square sheet of paper
Angle trisection is another of the classical problems that cannot be solved using a compass and straightedge but can be solved using origami. This does not include the trisection of a right angle, or construct an angle of thirty degrees, which is easy.
This construction was designed by Hisashi Abe. The angle omega is trisected by making folds l2 and l2 parallel to the base with l3 halfway in between the base and l2. Then point A is folded over to lie on line BA and at the same time point B is made to lie on line l3. Aligning the two points on the two lines is a neusis construction, similar to the construction of doubling the cube.
Origa-mathematical Diaspora

A modular floral origami piece
These seven axioms have galvanized mathematicians to view origami as a legitimate tool for geometric construction. As the ancient geometrical area of research has expanded, mathematicians have concocted more theory about the potential of paper folding. The implications for mathematics education are astounding: many proofs can arise from a simple straight crease. It would be invaluable to implement origami into high school geometry curricula due to the simplicity and versatility of paper folding.
Origami Inspiring Science and Vice Versa

Cover image of Takashi's Grandfather's notable origami piece
Takashi Satoh invents a time machine in the The Invisibles by Grant Morrison and uses it to send a cyborg from the future into the past so that she can save the world. While she is traveling through time with the time suit, she passes through 1945 Japan where Takashi's grandfather happens to be. His grandfather sees the time suit and this inspires him to design the origami piece that he then passes onto his grandson. This origami design later influences Takashi to build the time suit. In world of Morrison's book, origami acts as a mode of direct transmission of scientific ideas between two important characters. Similarly, contemporary society is making more explicit use of origami in the development of mathematics and its mode of instruction.
About the Creator
Sabine Lucile Scott
Hi! I am a twenty-nine year old college student at San Francisco State University majoring in Mathematics for Advanced Studies. I plan to continue onto graduate school in Mathematics once I am finished the plethora of courses which remain.






Comments
There are no comments for this story
Be the first to respond and start the conversation.